一个懒散的程序猿

130.被围绕的区域

题目可以转换成，从4个边界开始向内搜索字母 O，标记所有与它直接或间接相连的字母 O

int m,n;

void solve(vector<vector<char>>& board) {
    n = board.size();
    if (n == 0) return;
    m = board[0].size();

    for (int i = 0; i < n; i++) {
        dfs(board, i, 0);
        dfs(board, i, m - 1);
    }
    for (int i = 1; i < m - 1; i++) {
        dfs(board, 0, i);
        dfs(board, n - 1, i);
    }

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (board[i][j] == 'A') {
                board[i][j] = 'O';
            } else if (board[i][j] == 'O') {
                board[i][j] = 'X';
            }
        }
    }
}

void dfs(vector<vector<char>>& board, int x, int y) {
    if (x < 0 || x >= n || y < 0 || y >= m || board[x][y] != 'O') {
        return;
    }
    board[x][y] = 'A';
    dfs(board, x + 1, y);
    dfs(board, x - 1, y);
    dfs(board, x, y + 1);
    dfs(board, x, y - 1);
}

257.二叉树的所有路径

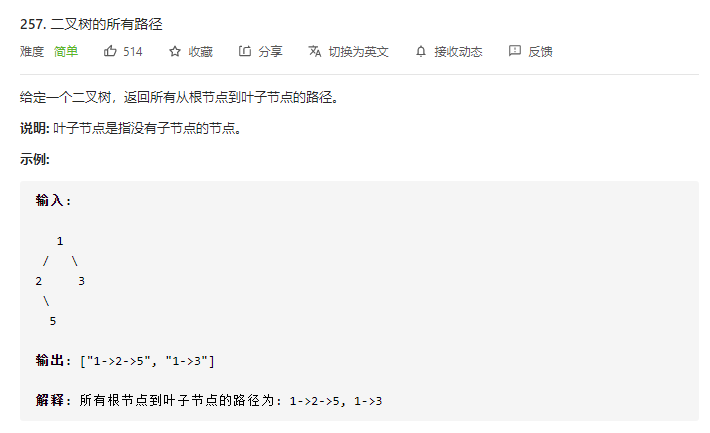
// 主函数
vector<string> binaryTreePaths(TreeNode* root) {
    vector<string> paths;
    dfs(root, "", paths);
    return paths;
}

// 辅函数
void dfs(TreeNode* root, string path, vector<string>& paths) {
    if (root != nullptr) {
        path += to_string(root->val);
        if (root->left == nullptr && root->right == nullptr) {  
            paths.push_back(path);                              
        } else {
            path += "->"; 
            dfs(root->left, path, paths);
            dfs(root->right, path, paths);
        }
    }
}

47.全排列 II

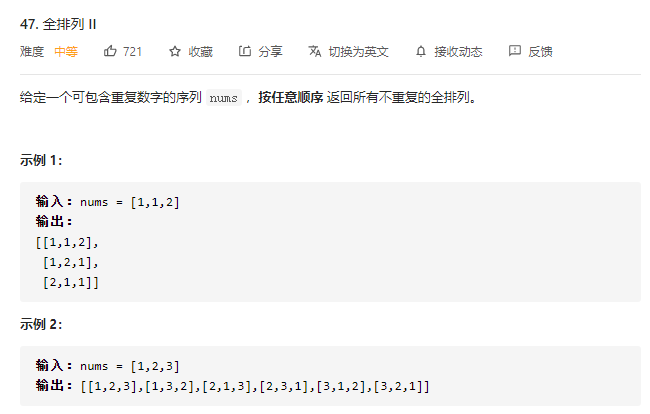
在 46,全排列 题目的基础上，序列中存在可重复的数字

去重一定要对元素经行排序，这样我们才方便通过相邻的节点来判断是否重复使用了

vector<int> vis;
// 辅函数
void backtrack(vector<int>& nums, vector<vector<int>>& ans, int idx, vector<int>& perm) {
    if (idx == nums.size()) {
        ans.emplace_back(perm);
        return;
    }
    for (int i = 0; i < (int)nums.size(); ++i) {
        if (vis[i] || (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])) {
            continue;
        }
        perm.emplace_back(nums[i]);
        vis[i] = 1;
        backtrack(nums, ans, idx + 1, perm);
        vis[i] = 0;
        perm.pop_back();
    }
}
// 主函数
vector<vector<int>> permuteUnique(vector<int>& nums) {
    vector<vector<int>> ans;
    vector<int> perm;
    vis.resize(nums.size());
    sort(nums.begin(), nums.end());
    backtrack(nums, ans, 0, perm);
    return ans;
}

40. 组合总和 II

37

310