图搜素算法,可以分为 2 种
- BFS 广度优先搜索
又译作宽度优先搜索,或横向优先搜索,是一种图形搜索算法。简单的说,BFS是从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。广度优先搜索的实现一般采用open-closed表。
从算法的观点,所有因为展开节点而得到的子节点都会被加进一个 先进先出 的队列中。一般的实现里,其邻居节点尚未被检验过的节点会被放置在一个被称为 open 的容器中(例如队列或是链表),而被检验过的节点则被放置在被称为 closed 的容器中。(open-closed表),所以简单看一下代码的实现
struct node {
int self; //数据
node *left; //左节点
node *right; //右节点
};
std::queue<node *> visited, unvisited;
node nodes[9];
node *current;
unvisited.push(&nodes[0]); // 先把root放入unvisited queue
while (!unvisited.empty()) { // 只有unvisited不空
current = (unvisited.front()); // 目前应该检验的
if (current->left != NULL)
unvisited.push(current->left); // 把左边放入queue中
if (current->right != NULL) // 右边压入。因为QUEUE是一个先进先出的结构,所以即使后面再压其他东西,依然会先访问这个。
unvisited.push(current->right);
visited.push(current);
cout << current->self << endl;
unvisited.pop();
}
- DFS 深度优先搜索
这个算法是一种用于遍历或搜索树或图的算法, 它会尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
深度优先搜索 这里用的是堆栈的结构,因为堆栈是一个 后进先出 的顺序。简单看一下代码的实现:
struct Node {
int self; // 数据
Node *left; // 左节点
Node *right; // 右节点
};
const int TREE_SIZE = 9;
std::stack<Node *> unvisited;
Node nodes[TREE_SIZE];
Node *current;
//初始化树
for (int i = 0; i < TREE_SIZE; i++) {
nodes[i].self = i;
int child = i * 2 + 1;
if (child < TREE_SIZE) // Left child
nodes[i].left = &nodes[child];
else
nodes[i].left = NULL;
child++;
if (child < TREE_SIZE) // Right child
nodes[i].right = &nodes[child];
else
nodes[i].right = NULL;
}
unvisited.push(&nodes[0]); //先把0放入 unvisited stack
// 树的深度优先搜索在二叉树的特例下,就是二叉树的先序遍历操作(这里是使用循环实现)
// 只有 unvisited 不空
while (!unvisited.empty()) {
current = (unvisited.top()); //当前应该访问的
unvisited.pop();
if (current->right != NULL)
unvisited.push(current->right );
if (current->left != NULL)
unvisited.push(current->left);
cout << current->self << endl;
}
还是做做题,感受感受
DFS 深度优先搜索
695.岛屿的最大面积
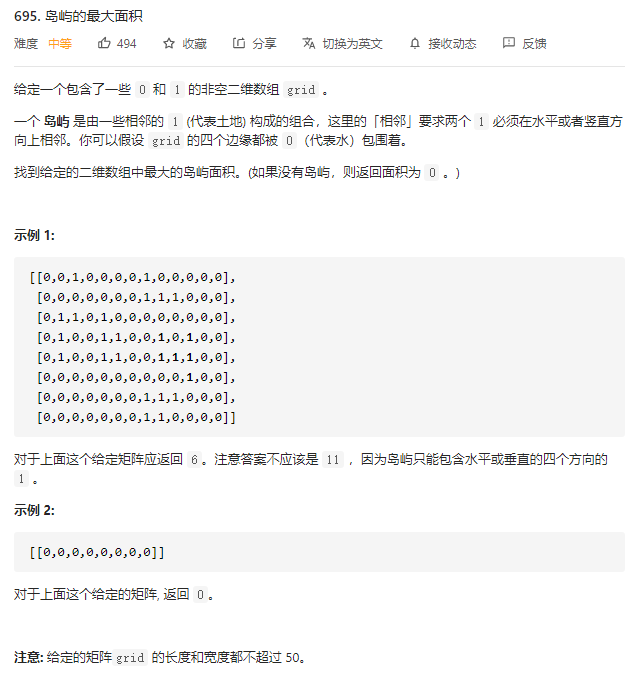
深度优先遍历
int getArea(vector<vector<int>>& grid, int i, int j)
{
// 判断边界
if (i == grid.size() || i < 0 || j == grid[0].size() || j < 0)
return 0;
if (grid[i][j] == 1)
{
grid[i][j] = 0;
// 该位置是岛屿,递归其上下左右
return 1 + getArea(grid, i + 1, j) + getArea(grid, i - 1, j ) + getArea(grid, i, j + 1) + getArea(grid, i, j - 1);
}
return 0;
}
int maxAreaOfIsland(vector<vector<int>>& grid) {
int area = 0;
for (int i = 0; i < grid.size(); i++)
for (int j = 0; j < grid[0].size(); j++)
if (grid[i][j] == 1)
area = max(area, getArea(grid, i, j) );
return area;
}
547.省份数量

和上一题差不多的逻辑,一行作为一个节点,将所有与该节点相连的节点置为已访问的属性(深度优先遍历),并归为一个省份
int findCircleNum(vector<vector<int>>& friends) {
int n = friends.size(), count = 0;
vector<bool> visited(n, false);
for (int i = 0; i < n; ++i) {
if (!visited[i]) {
dfs(friends, i, visited);
++count;
}
}
return count;
}
// 辅函数
void dfs(vector<vector<int>>& friends, int i, vector<bool>& visited) {
visited[i] = true;
for (int k = 0; k < friends.size(); ++k) {
if (friends[i][k] == 1 && !visited[k]) {
dfs(friends, k, visited);
}
}
}
417.水流问题

满足向下流能到达两个大洋的位置,如果我们对所有的位置进行搜索,那么在不剪枝的情况下复杂度会很高。
因此我们可以反过来想,从两个大洋开始向上流,这样我们只需要对矩形四条边进行搜索。
搜索完成后,只需遍历一遍矩阵,满足条件的位置即为两个大洋向上流都能到达的位置。
vector<int> direction{-1, 0, 1, 0, -1};
// 主函数
vector<vector<int>> pacificAtlantic(vector<vector<int>>& matrix) {
if (matrix.empty() || matrix[0].empty()) {
return {};
}
vector<vector<int>> ans;
int m = matrix.size(), n = matrix[0].size();
vector<vector<bool>> can_reach_p(m, vector<bool>(n, false));
vector<vector<bool>> can_reach_a(m, vector<bool>(n, false));
for (int i = 0; i < m; ++i) {
dfs(matrix, can_reach_p, i, 0);
dfs(matrix, can_reach_a, i, n - 1);
}
for (int i = 0; i < n; ++i) {
dfs(matrix, can_reach_p, 0, i);
dfs(matrix, can_reach_a, m - 1, i);
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; ++j) {
if (can_reach_p[i][j] && can_reach_a[i][j]) {
ans.push_back(vector<int>{i, j});
}
}
}
return ans;
}
// 辅函数
void dfs(const vector<vector<int>>& matrix, vector<vector<bool>>& can_reach, int r, int c) {
if (can_reach[r][c]) {
return;
}
can_reach[r][c] = true;
int x, y;
for (int i = 0; i < 4; ++i) {
x = r + direction[i], y = c + direction[i+1];
if (x >= 0 && x < matrix.size() && y >= 0 && y < matrix[0].size() &&
matrix[r][c] <= matrix[x][y] ) {
dfs(matrix, can_reach, x, y);
}
}
}
回溯法
46.全排列
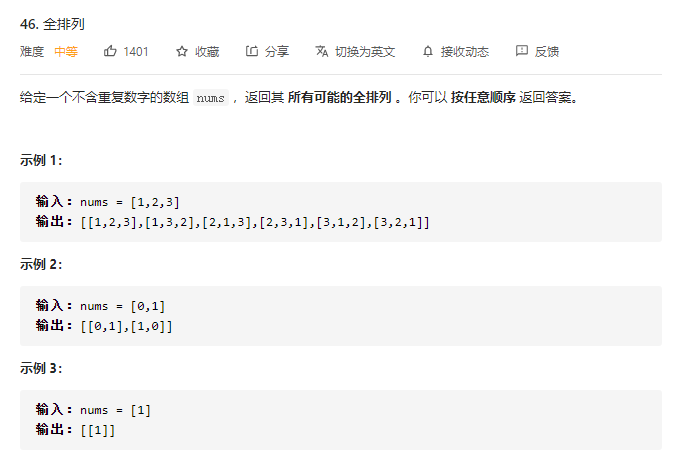
回溯法最典型的例子,第一次接触对我而言难度有点大,可以仔细看一下官方给的题解
https://leetcode-cn.com/problems/permutations/solution/quan-pai-lie-by-leetcode-solution-2/
// 主函数
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> ans;
backtracking(nums, 0, ans);
return ans;
}
// 辅函数
void backtracking(vector<int> &nums, int level, vector<vector<int>> &ans) {
if (level == nums.size() - 1) {
ans.push_back(nums);
return;
}
for (int i = level; i < nums.size(); i++) {
swap(nums[i], nums[level]); // 修改当前节点状态
backtracking(nums, level+1, ans); // 递归子节点
swap(nums[i], nums[level]); // 回改当前节点状态
}
}
77.组合
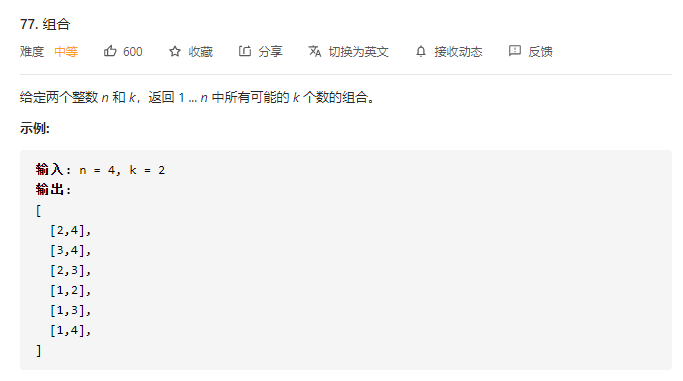
上一题差不多的思路,通过回溯试错的形式,决定是否把当前的数字加入结果中。
vector<vector<int>> combine(int n, int k) {
vector<vector<int>> ans;
vector<int> output(k,0);
// count 统计当前的 output 已经填入了几个值
int count = 0;
backtracking(ans, output, count, 1, n, k);
return ans;
}
void backtracking(vector<vector<int>> &ans, vector<int> &output,int& count, int pos, int n, int k) {
// 已经填了 k 个值就直接将 output 放入结果中
if (count == k) {
ans.push_back(output);
return;
}
for (int i = pos; i <= n; ++i) {
output[count++] = i; // 修改当前节点状态
backtracking(ans, output, count, i + 1, n, k); // 递归子节点
--count; // 回改当前节点状态
}
}
79.单词搜索

一个位置一个位置深度优先搜索,但是为了防止重复,引入一个和 board 同等大小的 visited 标识该位置是否被访问过
// 主函数
bool exist(vector<vector<char>>& board, string word) {
if (board.empty()) return false;
int m = board.size(), n = board[0].size();
vector<vector<bool>> visited(m, vector<bool>(n, false));
bool find = false;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
backtracking(i, j, board, word, find, visited, 0);
if (find)
return true;
}
}
return false;
}
// 辅函数
void backtracking(int i, int j, vector<vector<char>>& board, string& word, bool& find, vector<vector<bool>>& visited, int pos) {
// 边界检测
if (i < 0 || i >= board.size() || j < 0 || j >= board[0].size()) {
return;
}
// 当该位置访问过,或者已经找到 word, 或者目标位置值不相等
if (visited[i][j] || find || board[i][j] != word[pos]) {
return;
}
// 当能找到同样的 word 时候 find 设置为 true
if (pos == word.size() - 1) {
find = true;
return;
}
visited[i][j] = true; // 修改当前节点状态
// 递归子节点
backtracking(i + 1, j, board, word, find, visited, pos + 1);
backtracking(i - 1, j, board, word, find, visited, pos + 1);
backtracking(i, j + 1, board, word, find, visited, pos + 1);
backtracking(i, j - 1, board, word, find, visited, pos + 1);
visited[i][j] = false; // 回改当前节点状态
}
51.N 皇后
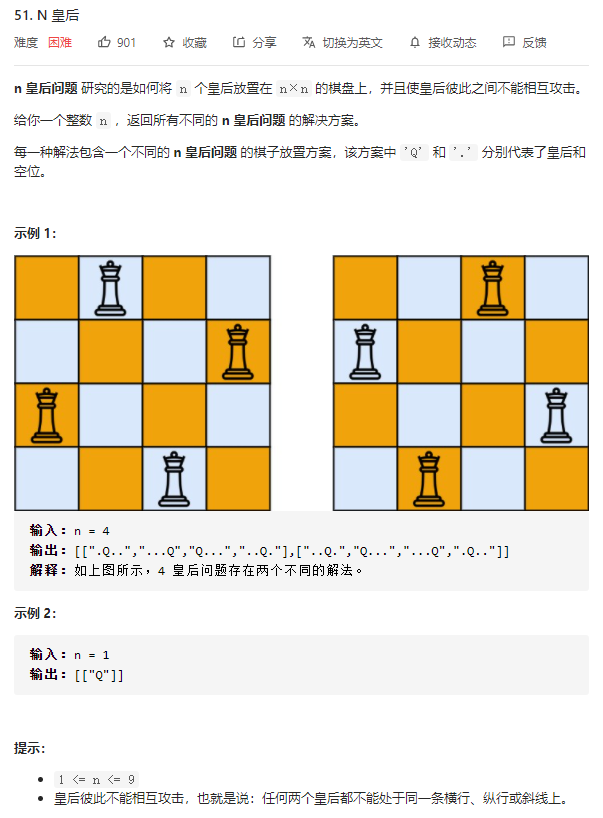
还是一个一个试错的过程,只是这次需要对每一行、列、左斜、右斜建立访问数组,来记录它们是否存在皇后。
// 主函数
vector<vector<string>> solveNQueens(int n) {
vector<vector<string>> ans;
if (n == 0) return ans;
vector<string> board(n, string(n, '.'));
vector<bool> column(n, false), ldiag(2*n-1, false), rdiag(2*n-1, false);
backtracking(ans, board, column, ldiag, rdiag, 0, n);
return ans;
}
// 辅函数
void backtracking(vector<vector<string>> &ans, vector<string> &board, vector<bool> &column, vector<bool> &ldiag, vector<bool> &rdiag, int row, int n) {
if (row == n) {
ans.push_back(board);
return;
}
for (int i = 0; i < n; ++i) {
if (column[i] || ldiag[n-row+i-1] || rdiag[row+i+1]) {
continue;
}
// 修改当前节点状态
board[row][i] = 'Q';
column[i] = ldiag[n-row+i-1] = rdiag[row+i+1] = true;
// 递归子节点
backtracking(ans, board, column, ldiag, rdiag, row+1, n);
// 回改当前节点状态
board[row][i] = '.';
column[i] = ldiag[n-row+i-1] = rdiag[row+i+1] = false;
}
}
广度优先搜索
934.最短的桥
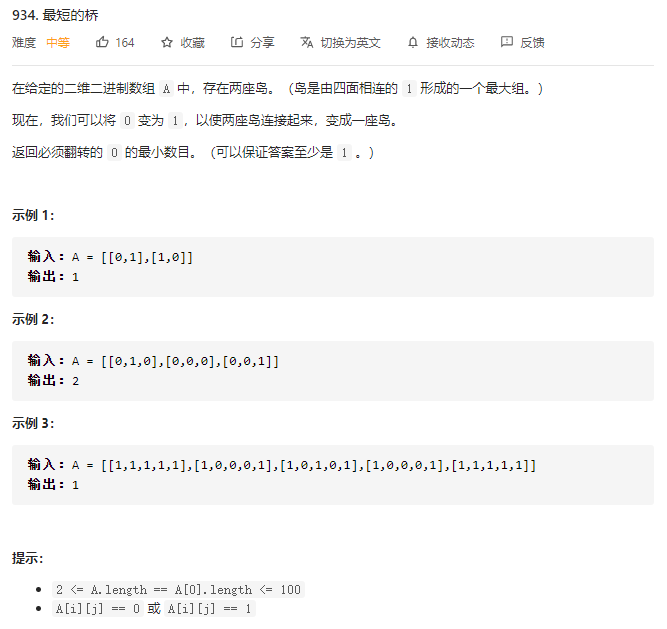
在寻找这两座岛时,我们使用深度优先搜索。在向外延伸时,我们使用广度优先搜索。
vector<int> direction{-1, 0, 1, 0, -1};
// 主函数
int shortestBridge(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
queue<pair<int, int>> points;
// dfs寻找第一个岛屿,并把1全部赋值为2
bool flipped = false;
for (int i = 0; i < m; ++i) {
// 找到第一个岛屿后就可以不用找了
if (flipped) break;
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) {
dfs(points, grid, m, n, i, j);
flipped = true;
break;
}
}
}
// bfs寻找第二个岛屿,并把过程中经过的0赋值为2,一层一层向外延伸,直到碰到第二个岛屿
int x, y;
int level = 0;
while (!points.empty()){
++level;
int n_points = points.size();
while (n_points--) {
auto [r, c] = points.front();
points.pop();
for (int k = 0; k < 4; ++k) {
x = r + direction[k], y = c + direction[k+1];
if (x >= 0 && y >= 0 && x < m && y < n) {
if (grid[x][y] == 2) {
continue;
}
if (grid[x][y] == 1) {
return level;
}
points.push({x, y});
grid[x][y] = 2;
}
}
}
}
return 0;
}
// 辅函数
void dfs(queue<pair<int, int>>& points, vector<vector<int>>& grid, int m, int n, int i, int j) {
if (i < 0 || j < 0 || i == m || j == n || grid[i][j] == 2) {
return;
}
if (grid[i][j] == 0) {
points.push({i, j});
return;
}
grid[i][j] = 2;
dfs(points, grid, m, n, i - 1, j);
dfs(points, grid, m, n, i + 1, j);
dfs(points, grid, m, n, i, j - 1);
dfs(points, grid, m, n, i, j + 1);
}
126.单词接龙 II

难度有点大,看看大佬的代码实现逻辑
我们可以把起始字符串、终止字符串、以及单词表里所有的字符串想象成节点。若两个字符串只有一个字符不同,那么它们相连。因为题目需要输出修改次数最少的所有修改方式,因此我们可以使用广度优先搜索,求得起始节点到终止节点的最短距离。
我们同时还使用了一个小技巧:我们并不是直接从起始节点进行广度优先搜索,直到找到终止节点为止;而是从起始节点和终止节点分别进行广度优先搜索,每次只延展当前层节点数最少的那一端,这样我们可以减少搜索的总结点数。举例来说,假设最短距离为 4,如果我们只从一端搜索 4 层,总遍历节点数最多是 1 + 2 + 4 + 8 + 16 = 31;而如果我们从两端各搜索两层,总遍历节点数最多只有 2 × (1 + 2 + 4) = 14。
在搜索结束后,我们还需要通过回溯法来重建所有可能的路径。
vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
vector<vector<string>> ans;
unordered_set<string> dict;
for (const auto &w : wordList)
dict.insert(w);
if (!dict.count(endWord))
return ans;
dict.erase(beginWord);
dict.erase(endWord);
unordered_set<string> q1{beginWord}, q2{endWord};
unordered_map<string, vector<string>> next;
bool reversed = false, found = false;
while ( !q1.empty()) {
unordered_set<string> q;
for (const auto &w : q1) {
string s = w;
for (size_t i=0; i<s.size(); i++) {
char ch = s[i];
for (int j=0; j<26; j++) {
s[i] = j + 'a';
if (q2.count(s)) {
reversed? next[s].push_back(w):next[w].push_back(s);
found = true;
}
if (dict.count(s)) {
reversed? next[s].push_back(w): next[w].push_back(s);
q.insert(s);
}
}
s[i] = ch;
}
}
if (found)
break;
for (const auto &w:q)
dict.erase(w);
if (q.size() <= q2.size()) {
q1 = q;
} else {
reversed = !reversed;
q1 = q2;
q2 = q;
}
}
if (found) {
vector<string> path = {beginWord};
backtracking(beginWord, endWord, next, path, ans);
}
return ans;
}
void backtracking(const string &src, const string &dst, unordered_map<string, vector<string>> &next, vector<string> &path, vector<vector<string>> &ans) {
if (src == dst) {
ans.push_back(path);
return;
}
for (const auto &s: next[src]) {
path.push_back(s);
backtracking(s, dst, next, path, ans);
path.pop_back();
}
}
总结
图和树的搜索这种类型的题难度挺大,主要就是涉及 BFS 广度优先搜索、DFS 深度优先搜索 以及 回溯法
在刷题过程中有 2 个点比较值得注意:
- 是通过直接在原数据上修改来记录访问状态,还是说需要额外创建一个
visited对象来保存访问过的状态 - 状态的维护格外需要注意
只能说这些题还需要反复体会体会~