查缺补漏-贪心算法

贪心算法 (greedy algorithm), 是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。
简单点说就是 保证每次操作都是局部最优的，从而使最后得到的结果是全局最优的。

做题是测试是否掌握的最好方式

455.分发饼干

455

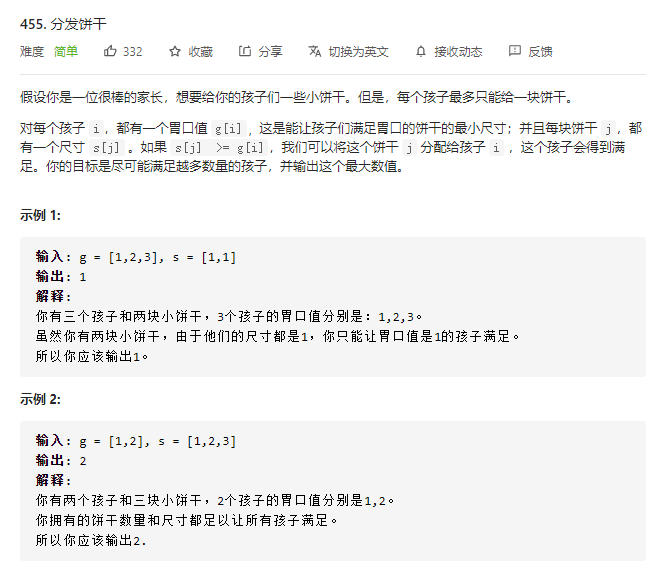
贪心策略：给剩余孩子里最小饥饿度的孩子分配最小的能饱腹的饼干。

int findContentChildren(vector<int>& children, vector<int>& cookies) {
    sort(children.begin(), children.end());
    sort(cookies.begin(), cookies.end());
    int child = 0, cookie = 0;
    while (child < children.size() && cookie < cookies.size()) {
        if (children[child] <= cookies[cookie]) ++child;
        ++cookie;
    }
    return child;
}

135.分发糖果

135

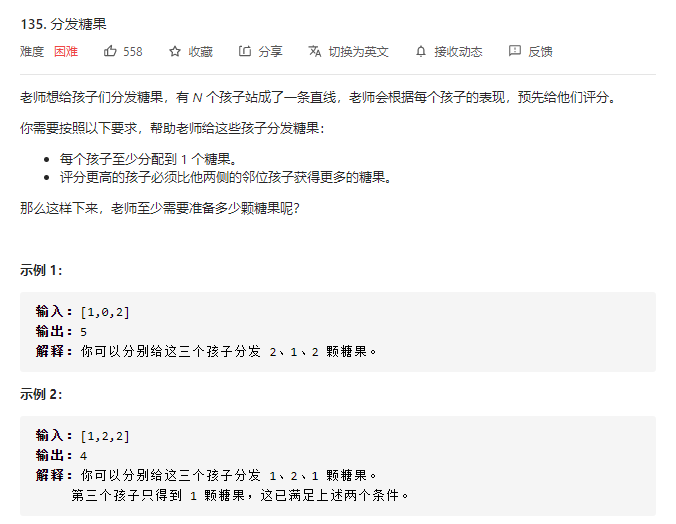
贪心策略：至少每人一个，一次循环仅考虑一侧大小关系

先从左往右遍历一遍，如果右边孩子的评分比左边的高，则右边孩子的糖果数更新为左边孩子的糖果数加 1；
再从右往左遍历一遍，如果左边孩子的评分比右边的高，且左边孩子当前的糖果数不大于右边孩子的糖果数，则左边孩子的糖果数更新为右边孩子的糖果数加 1

int candy(vector<int>& ratings) {
    int size = ratings.size();
    if (size < 2) return size;
    
    vector<int> num(size, 1);
    for (int i = 1; i < size; ++i) {
        if (ratings[i] > ratings[i-1]) 
            num[i] = num[i-1] + 1;
    }
    for (int i = size - 1; i > 0; --i) {
        if (ratings[i] < ratings[i-1]) 
            num[i-1] = max(num[i-1], num[i] + 1);
    }
    return accumulate(num.begin(), num.end(), 0); 
}

435.无重叠区间

435

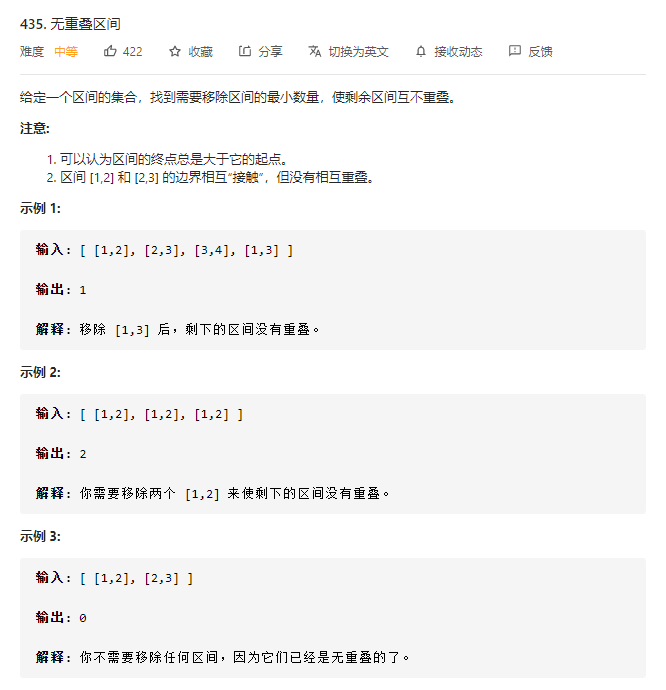
贪心策略：优先保留结尾小且不相交的区间。

先把区间按照结尾的大小进行增序排序，每次选择结尾最小且和前一个选择的区间不重叠的区间。

int eraseOverlapIntervals(vector<vector<int>>& intervals) {
    if (intervals.empty()) {
        return 0;
    }
    int n = intervals.size();
    sort(intervals.begin(), intervals.end(), [](vector<int> a, vector<int> b) {
        return a[1] < b[1];
    });
    int total = 0, prev = intervals[0][1];
    for (int i = 1; i < n; ++i) {
        if (intervals[i][0] < prev) {
            ++total;
        } else {
            prev = intervals[i][1];
        }
    }
    return total;
}

605.种花问题

605

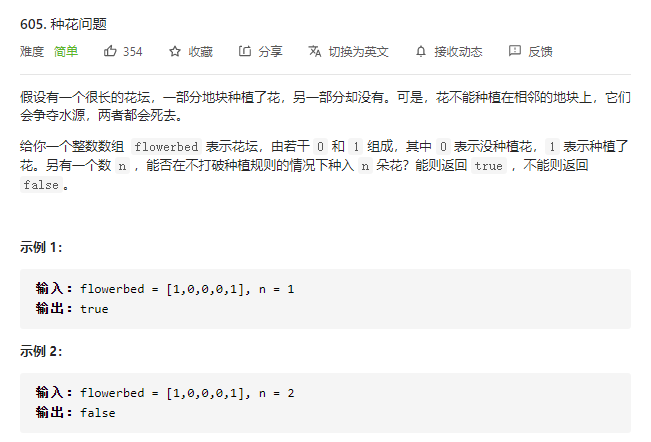
贪心策略：在不打破种植规则的情况下种入尽可能多的花，然后判断可以种入的花的最多数量是否大于或等于 n。

bool canPlaceFlowers(vector<int>& flowerbed, int n) {
    int length = flowerbed.size();  
    int count = 0;
    for (int i=0;i<length;i++) {
        if (flowerbed[i] == 0 
            &&  (i == length - 1 || flowerbed[i + 1] == 0)
            && (i == 0 || flowerbed[i - 1] == 0)) {
            flowerbed[i] = 1;
            count++;
        }
    }
    return count >= n;
}

452.用最少数量的箭引爆气球

452

贪心策略：最优保证所有气球中右边界位置最靠左的那一个被引爆

int findMinArrowShots(vector<vector<int>>& points) {
    if (points.empty()) {
        return 0;
    }
    sort(points.begin(), points.end(), [](const vector<int>& u, const vector<int>& v) {
        return u[1] < v[1];
    });
    int pos = points[0][1];
    int ans = 1;
    for (const vector<int>& balloon: points) {
        if (balloon[0] > pos) {
            pos = balloon[1];
            ++ans;
        }
    }
    return ans;
}

763.划分字母区间

763

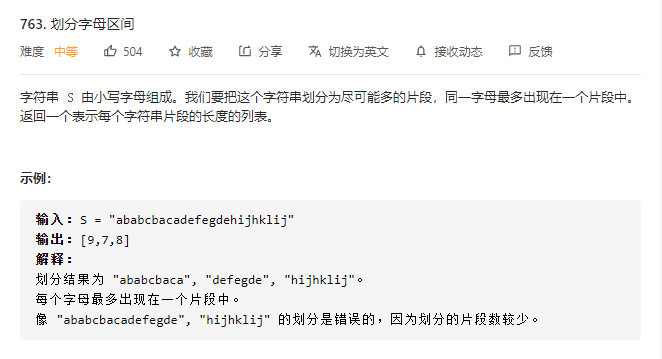
贪心策略：在得到每个字母最后一次出现的下标位置之后，可以使用贪心的方法将字符串划分为尽可能多的片段

vector<int> partitionLabels(string s) {
    int last[26];
    int length = s.size();
    for (int i = 0; i < length; i++) {
        last[s[i] - 'a'] = i;
    }
    vector<int> partition;
    int start = 0, end = 0;
    for (int i = 0; i < length; i++) {
        end = max(end, last[s[i] - 'a']);
        if (i == end) {
            partition.push_back(end - start + 1);
            start = end + 1;
        }
    }
    return partition;
}

122.买卖股票的最佳时间 II

122

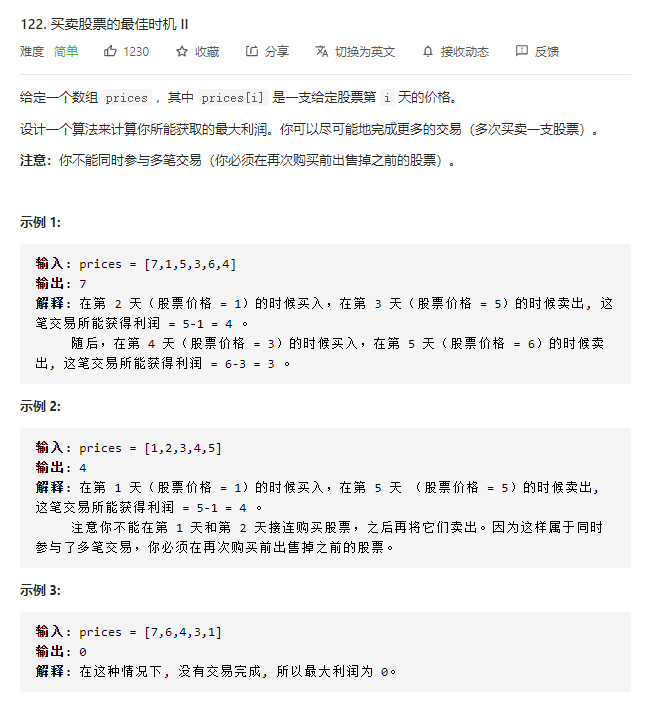
贪心策略：只要今天比昨天的价格高，就卖，计算利润

int maxProfit(vector<int>& prices) {
    int len = prices.size();
    if (len < 2) {
        return 0;
    }
    int res = 0;
    for (int i = 1; i < len; i++) {
        int diff = prices[i] - prices[i - 1];
        if (diff > 0) {
            res += diff;
        }
    }
    return res;
}

406.根据身高重建队列

406

贪心策略：身高从高到底排序，在配合身高大于等于人身高的个数插入到合适的位置

vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
    sort(people.begin(), people.end(), [](const vector<int>& u, const vector<int>& v) {
        return u[0] > v[0] || (u[0] == v[0] && u[1] < v[1]);
    });
    vector<vector<int>> ans;
    for (const vector<int>& person: people) {
        ans.insert(ans.begin() + person[1], person);
    }
    return ans;
}

665.非递减数列

665

贪心策略：在改变前后值大小的时候让数组 仍然维持非递减数列

简单点说，当 nums[i] > nums[i + 1]，要么

nums[i] = nums[i + 1] 前面的元素变小
nums[i + 1] = nums[i] 后面的元素变大

bool checkPossibility(vector<int> &nums) {
    int n = nums.size();
    for (int i = 0; i < n - 1; ++i) {
        int x = nums[i], y = nums[i + 1];
        if (x > y) {
            // 尝试前面元素变小
            nums[i] = y;
            // 通过排序判断是否是递增
            if (is_sorted(nums.begin(), nums.end())) {
                return true;
            } 
            // 如果前面元素变小不行，尝试换成后面元素变大
            nums[i] = x; 
            nums[i + 1] = x;
            return is_sorted(nums.begin(), nums.end());
        }
    }
    return true;
}

一个懒散的程序猿