一个懒散的程序猿

双指针 主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。也可以延伸到多个数组的多个指针。
若两个指针指向同一数组，遍历方向相同且不会相交，则也称为滑动窗口（两个指针包围的区域即为当前的窗口），经常用于区间搜索。
若两个指针指向同一数组，但是遍历方向相反，则可以用来进行搜索，待搜索的数组往往是排好序的。

刷刷题，刷刷题

167.两数之和 II - 输入有序数组

策略: 因为已经是排好序的输入,可以头尾双指针向中间移动

vector<int> twoSum(vector<int>& numbers, int target) {
    int l = 0, r = numbers.size() - 1, sum;
    while (l < r) {
        sum = numbers[l] + numbers[r];
        if (sum == target) break;
        if (sum < target) ++l;
        else --r;
    }
    return vector<int>{l + 1, r + 1};
}

88.合并两个有序数组

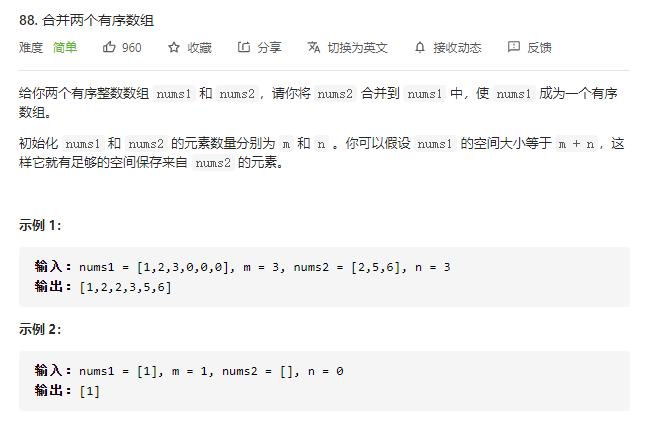
策略: 两个数组已经排好序，把两个指针分别放在两个数组的末尾，将较大值放到第一个数组末端

void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    int pos = m-- + n-- - 1;
    while (m >= 0 && n >= 0) {
        nums1[pos--] = nums1[m] > nums2[n]? nums1[m--]: nums2[n--];
    }
    while (n >= 0) {
        nums1[pos--] = nums2[n--];
    }
}

142.环形链表 II

策略:

• 给定两个指针，分别命名为 slow 和 fast，起始位置在链表的开头。每次 fast 前进两步，slow 前进一步。
  
• 如果 fast 可以走到尽头，那么说明没有环路；如果 fast 可以无限走下去，那么说明一定有环路，且一定存在一个时刻 slow 和 fast 相遇。
  
• 当 slow 和 fast 第一次相遇时，我们将 fast 重新移动到链表开头，并让 slow 和 fast 每次都前进一步。当 slow 和 fast 第二次相遇时，相遇的节点即为环路的开始点

ListNode *detectCycle(ListNode *head) {
    ListNode *slow = head, *fast = head;
    // 判断是否存在环路
    do {
        if (!fast || !fast->next) return nullptr;
        fast = fast->next->next;
        slow = slow->next;
    } while (fast != slow);
    // 如果存在，查找环路节点
    fast = head;
    while (fast != slow){
        slow = slow->next;
        fast = fast->next;
    }
    return fast;
}

76.最小覆盖子串

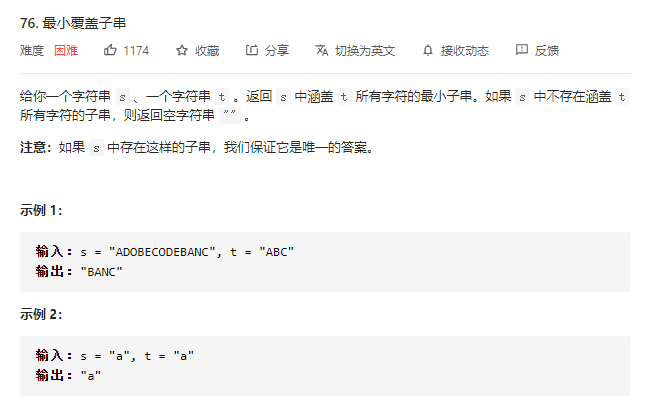
策略: 使用一个滑动窗口, 搜索最短子字符串

第一次接触，难度有点大，可以参考一下官方的视频解析

https://leetcode-cn.com/problems/minimum-window-substring/solution/zui-xiao-fu-gai-zi-chuan-by-leetcode-solution/

string minWindow(string S, string T) {
    vector<int> chars(128, 0);
    vector<bool> flag(128, false);
    // 先统计T中的字符情况
    for(int i = 0; i < T.size(); ++i) {
        flag[T[i]] = true;
        ++chars[T[i]];
    }
    // 移动滑动窗口，不断更改统计数据
    int cnt = 0, left = 0, min_left = 0, min_size = S.size() + 1;
    for (int right = 0; right < S.size(); ++right) {
        if (flag[S[right]]) {
            if (--chars[S[right]] >= 0) {
                ++cnt;
            }
            // 若目前滑动窗口已包含T中全部字符，
            // 则尝试将l右移，在不影响结果的情况下获得最短子字符串
            while (cnt == T.size()) {
                if (right - left + 1 < min_size) {
                    min_left = left;
                    min_size = right - left + 1;
                }
                if (flag[S[left]] && ++chars[S[left]] > 0) {
                    --cnt;
                }
                ++left;
            }
        }
    }
    return min_size > S.size()? "": S.substr(min_left, min_size);
}

633.平方数之和

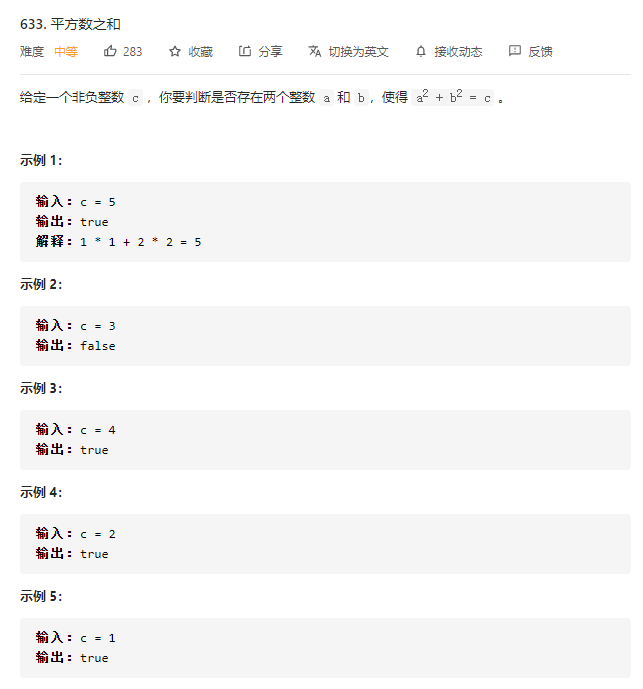
策略： 双指针从 [0, (int)sqrt(c)] 向中间移动

bool judgeSquareSum(int c) {
    long left = 0;
    long right = (int)sqrt(c);
    while (left <= right) {
        long sum = left * left + right * right;
        if (sum == c) {
            return true;
        } else if (sum > c) {
            right--;
        } else {
            left++;
        }
    }
    return false;
}

680.验证回文字符串 Ⅱ

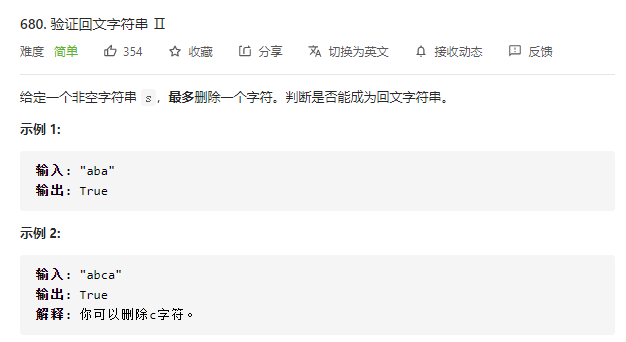
策略：双指针从两头开始向中间遍历，删除一个元素时需要考虑删除左边还是右边

bool checkPalindrome(const string& s, int low, int high) {
    for (int i = low, j = high; i < j; ++i, --j) {
        if (s[i] != s[j]) {
            return false;
        }
    }
    return true;
}

bool validPalindrome(string s) {
    int low = 0, high = s.size() - 1;
    while (low < high) {
        char c1 = s[low], c2 = s[high];
        if (c1 == c2) {
            ++low;
            --high;
        } else {
            return checkPalindrome(s, low, high - 1) || checkPalindrome(s, low + 1, high);
        }
    }
    return true;
}

524.通过删除字母匹配到字典里最长单词

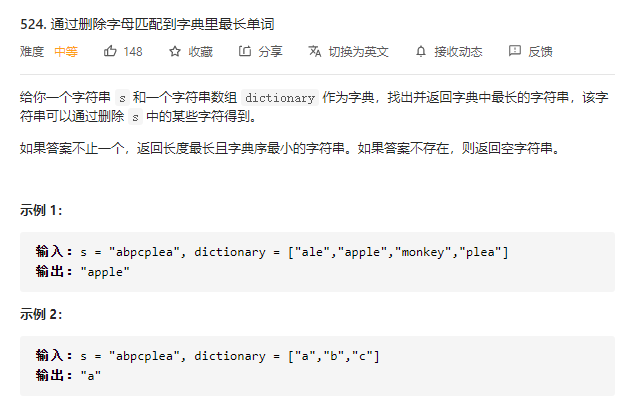
策略：使用双指针遍历2个字符串，判断子串是否被包含

bool judgeContains(string &s, string &t) {
    int sp=0,tp=0;
    while ( sp<s.size() && tp<t.size()) {
        if ( s[sp] == t[tp] ) {
            tp++;
        } 
        sp++;
    }

    return tp == t.size();
}

string findLongestWord(string s, vector<string>& dictionary) {
    sort(dictionary.begin(), dictionary.end(),[](const string &a, const string &b){
        return a.size() == b.size()?  a < b : a.size() > b.size();
    });

    for (int i = 0; i< dictionary.size(); ++i) {
        string target = dictionary[i];
        bool contains = judgeContains(s, target);
        if (contains)
            return target;
    }
    return "";
}

340.至多包含 K 个不同字符的最长子串

策略：典型的滑动窗口双指针技巧

int lengthOfLongestSubstringKDistinct(string s, int k) {
    unordered_map<char,int> m;
    int maxlen = 0;
    for(int i = 0, j = 0; i < s.size(); ++i)
    {
        if(m.size() <= k)
            m[s[i]]++;
        while(m.size()>k)
        {
            if(--m[s[j]] == 0)
                m.erase(s[j]);
            j++;
        }
        maxlen = max(maxlen, i-j+1);
    }
    return maxlen;
}