二分查找也常被称为 二分法 或者 折半查找,每次查找时通过将待查找区间分成两部分并只取一部分继续查找,将查找的复杂度大大减少。对于一个长度为 O(n) 的数组,二分查找的时间复杂度为 O(logn)。
实现的代码很简单,简单看一下实现
// 二分查找(折半查找):对于已排序,若无序,需要先排序
// 非递归
int BinarySearch(vector<int> v, int value , int low, int high) {
if (v.size() <= 0) {
return -1;
}
while (low <= high) {
int mid = low + (high - low) / 2;
if (v[mid] == value) {
return mid;
}
else if (v[mid] > value) {
high = mid - 1;
}
else {
low = mid + 1;
}
}
return -1;
}
// 递归
int BinarySearch2(vector<int> v, int value, int low, int high)
{
if (low > high)
return -1;
int mid = low + (high - low) / 2;
if (v[mid] == value)
return mid;
else if (v[mid] > value)
return BinarySearch2(v, value, low, mid - 1);
else
return BinarySearch2(v, value, mid + 1, high);
}
还是做一做题详细体会一下~
69.x 的平方根
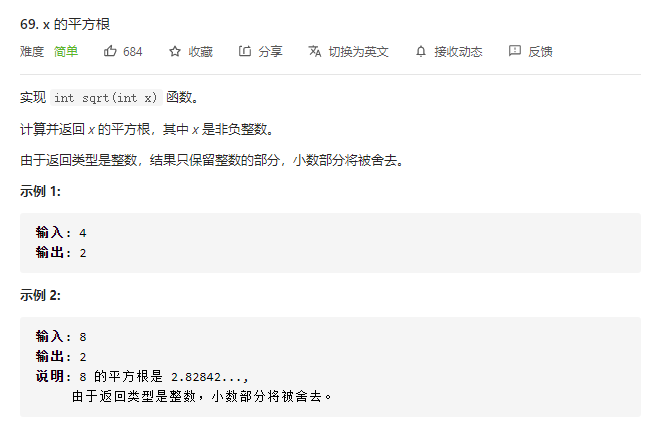
策略:很简单的二分查找,但是需要注意边界处理,比如 0 和 整数部分
int mySqrt(int a) {
if (a == 0) return a;
int l = 1, r = a, mid, sqrt;
while (l <= r) {
mid = l + (r - l) / 2;
sqrt = a / mid;
if (sqrt == mid) {
return mid;
} else if (mid > sqrt) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return r;
}
34.在排序数组中查找元素的第一个和最后一个位置
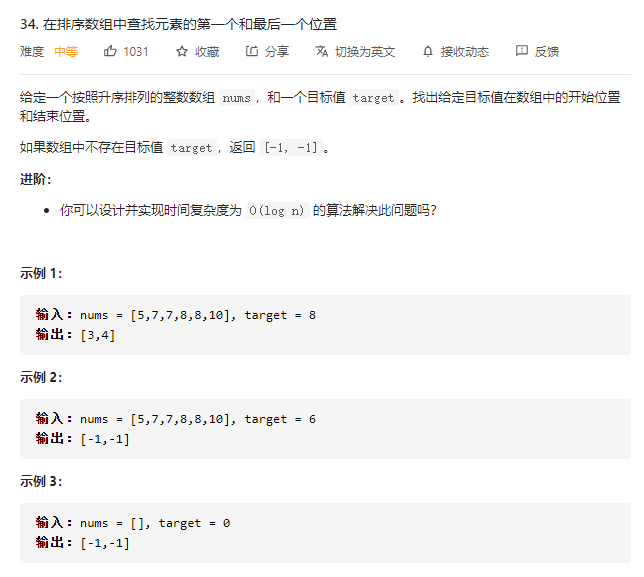
策略:二分查找一个重复元素的边界问题,需要额外注意
vector<int> searchRange(vector<int>& nums, int target) {
if (nums.empty()) return vector<int>{-1, -1};
int lower = lower_bound(nums, target);
int upper = upper_bound(nums, target) - 1;
if (lower == nums.size() || nums[lower] != target) {
return vector<int>{-1, -1};
}
return vector<int>{lower, upper};
}
int lower_bound(vector<int> &nums, int target) {
int l = 0, r = nums.size(), mid;
while (l < r) {
mid = (l + r) / 2;
if (nums[mid] >= target) {
r = mid;
} else {
l = mid + 1;
}
}
return l;
}
int upper_bound(vector<int> &nums, int target) {
int l = 0, r = nums.size(), mid;
while (l < r) {
mid = (l + r) / 2;
if (nums[mid] > target) {
r = mid;
} else {
l = mid + 1;
}
}
return l;
}
81.搜索旋转排序数组 II
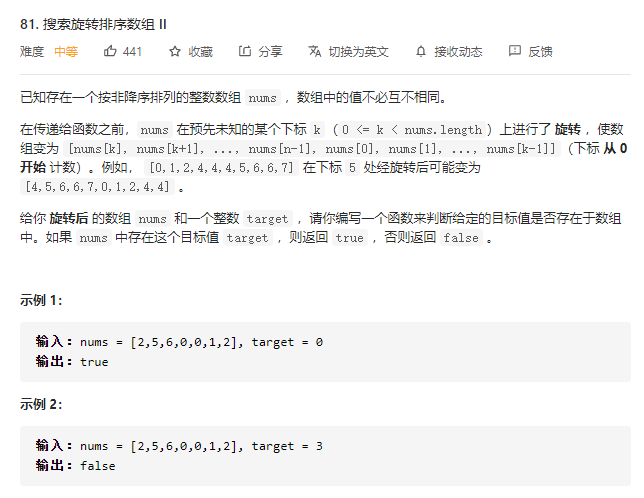
策略:题目中对旋转的解释其实和它题解中的解释是有出入的,实际这道题的意思是, 例如 nums=[0,1,4,4,5,6,7], 旋转第一个 4, 是将第一个数字 4 后面的有序数组挪到原数组前面,也就是变成了 [4,5,6,7,0,1,4]
按照这个思路,二分的思路就需要想办法逐步缩小最小值所在的范围,只要使用 mid 不停和最右边的值进行比较即可,毕竟右边是部分有序的
bool search(vector<int>& nums, int target) {
int start = 0, end = nums.size() - 1;
while (start <= end) {
int mid = (start + end) / 2;
if (nums[mid] == target) {
return true;
}
if (nums[start] == nums[mid]) {
// 无法判断哪个区间是增序的
++start;
} else if (nums[mid] <= nums[end]) {
// 右区间是增序的
if (target > nums[mid] && target <= nums[end]) {
start = mid + 1;
} else {
end = mid - 1;
}
} else {
// 左区间是增序的
if (target >= nums[start] && target < nums[mid]) {
end = mid - 1;
} else {
start = mid + 1;
}
}
}
return false;
}
其实暴力的 for 循环最起码代码简单很多,但是时间复杂度就不能到 O(log(n))~
154.寻找旋转排序数组中的最小值 II

策略:还是想办法逐步搜小最小值所在的范围,只要使用 mid 不同和最右边的值进行比较即可
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] < nums[right]) {
right = mid;
}
else if (nums[mid] > nums[right]) {
left = mid + 1;
}
else {
right --;
}
}
return nums[left];
}
};
540.有序数组中的单一元素
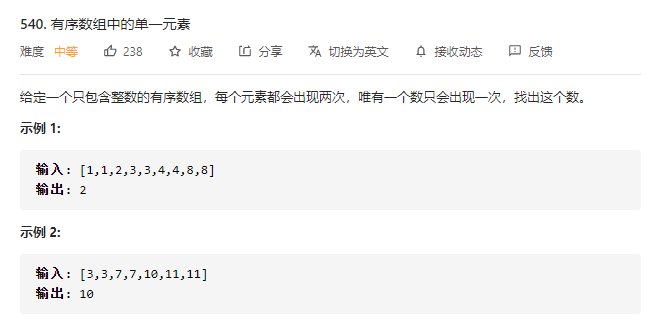
策略:根据独立数出现前后,奇偶位置比较的变化,决定 left 和 right 如何变化
int singleNonDuplicate(vector<int>& nums) {
int left = 0, right = nums.size() - 1;
while (left < right) {
int mid = left + (right-left)/2;
if ( mid%2 == 0) {
if (nums[mid] == nums[mid+1]) {
left = mid+1;
} else {
right = mid;
}
} else {
if ( nums[mid] == nums[mid-1]) {
left = mid+1;
} else {
right = mid;
}
}
}
return nums[left];
}
4.寻找两个正序数组的中位数

下意识的想到先把两个数组合并,然后根据总长度的奇偶,来决定返回的中位数值,但是要设计一个时间复杂度为 O(log(m+n)) 的算法解决此问题, 肯定要用二分查找的方法。
官方提供的二分思路很有意思,将原本找中位数,变成找第 k 小的数,每次二分之后,移除不可能是第 k 小的元素,通过修正 k 这个目标,直到出现 边界情况 或者 k=1 时, 找出剩余数组中的第 k 个元素
int getKth(const vector<int>& nums1, const vector<int>& nums2, int k) {
/* 主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
* 这里的 "/" 表示整除
* nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
* nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
* 取 pivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
* 这样 pivot 本身最大也只能是第 k-1 小的元素
* 如果 pivot = pivot1,那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums1 数组
* 如果 pivot = pivot2,那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums2 数组
* 由于我们 "删除" 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数
*/
int m = nums1.size();
int n = nums2.size();
int index1 = 0, index2 = 0;
while (true) {
// 边界情况
if (index1 == m) {
return nums2[index2 + k - 1];
}
if (index2 == n) {
return nums1[index1 + k - 1];
}
if (k == 1) {
return min(nums1[index1], nums2[index2]);
}
// 正常情况
int newIndex1 = min(index1 + k / 2 - 1, m - 1);
int newIndex2 = min(index2 + k / 2 - 1, n - 1);
int pivot1 = nums1[newIndex1];
int pivot2 = nums2[newIndex2];
if (pivot1 <= pivot2) {
k -= newIndex1 - index1 + 1;
index1 = newIndex1 + 1;
}
else {
k -= newIndex2 - index2 + 1;
index2 = newIndex2 + 1;
}
}
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int totalLength = nums1.size() + nums2.size();
if (totalLength % 2 == 1) {
return getKth(nums1, nums2, (totalLength + 1) / 2);
}
else {
return (getKth(nums1, nums2, totalLength / 2) + getKth(nums1, nums2, totalLength / 2 + 1)) / 2.0;
}
}
总结
二分查找有2个前提 有序 且是 顺序 数组,这个有序只是为了便于我们缩小区间,所以数组可以不是完全有序,只要能够在判断后删除不可能的一半区间即可,循环,直到得到结果~